Percorso Curricolare 2
“Dai pentamini alle regolarità nei solidi”
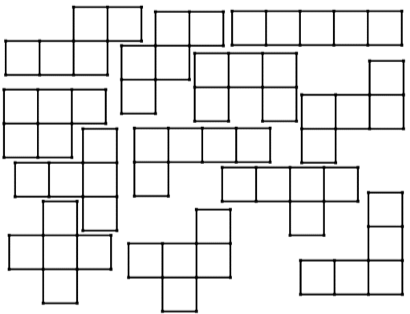
Pentamini, esamini, cubo, dado e viceversa
Il seguente percorso può ritenersi formato da parti componibili e perciò utilizzabili tutte nella successione proposta; oppure come attività singole da inserire in un progetto di geometria piana e solida. I contenuti riguardano l’esaedro come dado da gioco e come cubo, sezioni, sviluppi, regolarità aritmetiche e loro generalizzazione.

Partire da punto, retta e piano è fondamentale per una trattazione razionale ma meno comprensibile e meno motivante per gli alunni.
La rigorosa geometria di Euclide deve essere il punto di arrivo della costruzione della conoscenza matematica nel percorso scolastico dell’alunno
Il sapere deve passare per una trasposizione didattica adattata ai livelli scolastici che ci interessano.
Ciascuna delle attività di questo percorso è rivolta ad una o più classi di riferimento e quindi calibrata nello scenario, negli obiettivi matematici, nella gestione laboratoriale e nelle conclusioni, all’età degli alunni; ma tutte partono da un problema che richiede la formulazione di congetture individuali, il confronto tra pari nel gruppo e la discussione di classe sulle soluzioni e sulle strategie trovate.
Le indicazioni metodologiche e il contesto suggeriti tendono a porre l’alunno nella condizione di “risolutore di problemi” e invitano l’insegnante a costruire nel gruppo-classe un clima di laboratorio che consenta una condivisione consapevole delle nuove conoscenze matematiche costruite.


Il lavoro di gruppo, le fasi di discussione collettiva tra pari e con l’insegnante sono modalità necessarie di organizzazione didattica. Le fasi di conclusione delle diverse attività che compongono il percorso mirano alla integrazione degli interventi e apporti degli alunni rispetto agli obiettivi e alle finalità di ciascuna attività.
Si riportano in sintesi l’articolazione e la descrizione delle attività previste per ciascuna delle fasce d’età, cui seguono le schede di lavoro da proporre nelle fasi individuali e/o di gruppo del laboratorio.
Per verificarne la validità, le parti del percorso sono state più volte sperimentate nella scuola primaria e secondaria di primo grado.
La facilità nella preparazione o nel reperimento dei materiali richiesti fa considerare la nostra sperimentazione ripetibile e adattabile in tutti i contesti scolastici.